音色への動学的アプローチ
楽器の「音色」はスペクトルによって特徴づけられている・・・音に科学的な興味を持つ多くの人がこのようなイメージを持っているのではないでしょうか?
例として、ヴァイオリンと歌声のスペクトル(ソナグラム)例を掲げます。私たちは、これらが適切に示している響きの側面と、ここでは死角になってしまう別の面があることに注意したいと考えました。
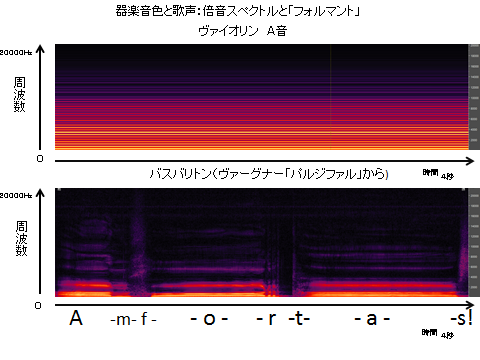
器楽音(ヴァイオリン)と歌声(ヴァーグナー「パルジファル」から)のスペクトル(ソナグラム)例
<やや専門的な補足>
私たち人間は時間の流れに沿って音を聴きます。一方スペクトル=フーリエ変換の世界は、ある短い時間幅で音響データを切り出し、ここに周期性を仮定して計算されます。やや標語的に書くなら、スペクトルの世界は「静的」(時間が流れない)で「線形」(正弦波を基底に表現)かつ時間的に「可逆」(周期性を前提)なモデルとして切り出したものと言えます。
これに対し、現実世界で生きる私たちの聴取の経験は動的(時間に沿って変化)で「非線形」(帯域雑音的)かつしばしば時間的に不可逆(言語音声を録音したテープを逆回しすれば多くの子音が時間的に不可逆なプロセスとすぐに判るでしょう)です。
例えばヴァイオリンは弦が共鳴胴に張られており、豊かな響きの中にはエコーが含まれています。電子的に音作りする際には遅延回路(ディレイ)で実現されるこうしたプロセスをスペクトルは能く記述しません。
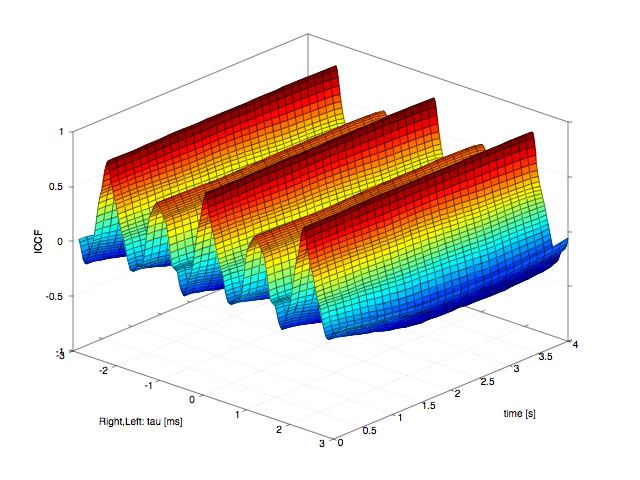
ヴァイオリン音色の3Dコレログラム
上では時間的に推移するヴァイオリン音色の3Dコレログラムの一例で、従来議論されてこなかったエコーの成分がわかり易く見えています。下ではホール内に響く歌声の相関解析結果が時間的にどのように推移するかを確認することが出来ます。
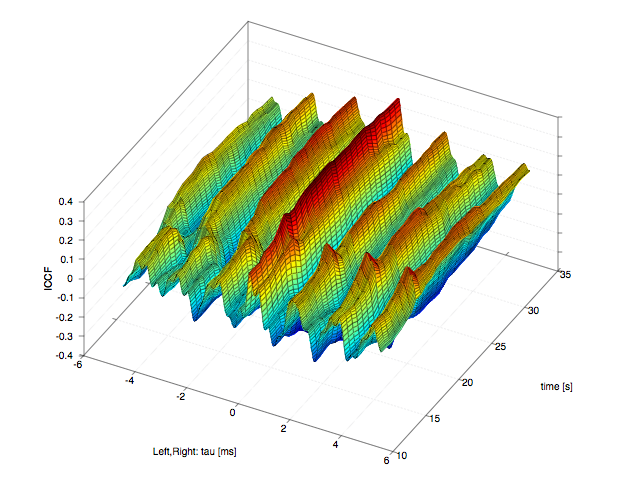
ホール内に響く歌声の3Dコレログラム